A. EINSTEIN'S ERRORS ANALYZED WITH LORENTZ'S TRANSFORMATION FORMULAS

PRESENTATION

Reading in A. Einstein's book entitled: “On the theory of special and general relativity” the topic of the Lorentz Transformation Formulas, some doubts have arisen. Having analyzed these doubts, we have seen that they come from two errors. These are the same errors that we already exposed in our previous essays, in which we denounced that through relative movements the author of the aforementioned book confused the verb SEE with the verb BE. And, thus, we ironically say that he preaches “the miracle of transmutation.”

We dedicate this essay to highlighting the aforementioned errors and to proposing a method of analysis to construct and interpret the aforementioned formulas. For better follow-up of this study, we have divided it into two parts. The second part is somewhat more theoretical than the first and some mathematical developments appear.

FIRST PART

In this first part we will propose and explain the steps to follow for the construction of the Lorentz Transformation Formulas. We will call these formulas: “Formulas of the VISION of the Extension of an event observed from a mobile platform”, in order to correct the distorted acceptance between the verbs: SEE and BE.

1.- AN EXPLANATION THAT APPEARS IN A BOOK BY A. EINSTEIN

In the book “On the theory of special and general relativity” by Einstein, on page 32 (Edition “Alianza Editorial”), he describes the form and usefulness of the formulas called Lorentz Transformations, as follows:

“Given the quantities (x,y,z,t) of an event with respect to (k), what are the values (x`,y`,z´,t´) of the same event with respect to (k´)?

The relations must be chosen in such a way that they satisfy the laws of light propagation in a vacuum for one and the same ray of light (and also for any ray of light) with respect to (K) and (K´).”

And he goes on to say:
“The problem is solved by the equations”
Space Formula

Formula of Time

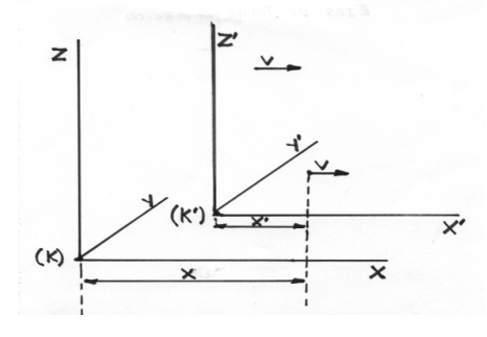
And, on this same page of the aforementioned book, the following coordinate system (k) and (K) is drawn.

Figure 1

Later we will demonstrate that the expression: (v×X)/c² that appears in the time formula, translates as a time and that with the “space formula” there would be enough to make “theoretical” applications.

2.- WHERE DO WE FIND ERRORS IN THE EXPLANATION GIVED BY A. EINSTEIN IN THE LORENTZ TRANSFORMATION FORMULA?

The first error we found in the explanations given by the Physicist about the Formulas and Lorentz Transformations is the following:

When asking:

What are the values (x`,y`,z´,t´) of the same event with respect to (k´)?

We believe that you are thinking about “transformation” or “converting” rather than SEEING the event from a mobile platform regarding the event. We believe this is one of the errors. He falls back into the error that we have already commented on in previous of our essays. Through relative movements he confuses the verb SEE with the verb BE. In this way he prepares what we have called “the miracle of transmutation”. We say that he is thinking about the “transformation” since in the mental experiment of the bar for measuring lengths, subjected to a relative movement, he applies the formula for the transformation of space and preaches the nonsense of the shortening of the aforementioned bar. This error consists of believing in the “transformation” of matter.

The second mistake consists of wanting to apply the conclusions drawn in a mental experiment to a real-life physical experiment.

We wonder if the results obtained from a thought experiment can be applicable in real life.

We believe that the answer has to be negative. Precisely, the problem is reasoned by applying a mental experiment because it is not possible to apply a physical experiment. And, so far, it seems that it is a chimera to try to build a physical experiment that transcribes the results of a mental experiment. All this is aggravated if in the mental experiment the action of SEE has been confused with the verb BE.

In this essay we will see that the expression will appear.

In which (v) is the speed of a moving body and (c) is the speed of light. Even considering (v) one of the greatest speeds in our real world, for example the speed of a space rocket, its speed is so small with respect to that of light (c) that the quotient that appears within the radical of the expression that we have written would be an infinite value. That is why we say that, as we will see, it would be a chimera to transfer it to a physical experiment.

(NOTE: Do not confuse, as A. Einstein states, that the limit speed that can be reached is the speed of light. The reader can read the essay contained in our Blog, titled: “Theory of relativity. - It is possible that a particle can travel at a speed faster than light." Note that there we are talking about a particle and not a body endowed with movement.)

3.- WHAT DO WE UNDERSTAND BY THE DIMENSION OF AN EVENT?

We will understand the dimension of an event as its duration from its appearance until its extinction. We can value this duration in length or time. We will call this dimension EXTENSION of the event.

4.- WE ASKED, IN A THEORETICAL APPROACH, WHAT WOULD TRANSFORMATION FORMULAS BE USED FOR?

According to our approach we will say that its purpose would be: Assess the dimension of an event, which occurs in a certain position in space, by an observer who is moving at a constant and rectilinear speed (v) with respect to this event.

(NOTE: The reader should note that we are talking about a “theoretical” approach. At the end we will explain that this approach, using mathematical resources, could hardly be applied in our real life)

5.- FORMULA FOR THE TRANSFORMATION OF THE VISION OF THE EXTENSION OF AN EVENT

In order not to confuse with the erroneous purpose that Einstein intends to give to the Lorentz transformation formulas, in our analysis we will call them: Transformation formulas of the VISION of the Extension of an event. The reader should note that we highlight the verb SEE.

6.- ACTIONS IMPLIED IN THE TRANSFORMATION OF THE VISION OF THE EXTENSION OF AN EVENT

To build the “formula for the transformation of the VISION of the Extension of an event”, in our study we will consider three actions implicit in it. These actions are the following:

APPEAR the event; REMAIN your visibility; SEE your Extension.

7.- TWO PHYSICAL PHENOMENA TO CONSIDER

When constructing the transformation formula we must take into account that two physical phenomena overlap. One is the movement and displacement of the observer of the event at a speed (v). The other physical phenomenon is the VISION of the event, from the place where the observer has moved, and in which the speed of light is involved (c).

8.- A RIGHT TRIANGLE TO ANALYZE THE VISION OF THE EXTENSION OF AN EVENT FROM A MOBILE PLATFORM

To analyze the VISION of the Extension of an event from a mobile platform we will use a right-angled triangle.

We must define the situation of three points representative of: Appearance of the event (E); Completion of the Extension of the event (F) and Observation of the event (O). With these three
points we define a triangle

9.- WHY SHOULD THE TRIANGLE BE RECTANGLE?

To position the event and its observation position in space, we will consider the two legs of the triangle as coordinate axes. The legs of the triangle must be perpendicular to each other. This is so since:
On the horizontal axis we will give the meaning as the path of the movement and the speed (v), and on the vertical axis we will express the dimension of the Extension of the event. Without going into more specialized mathematical expressions, we only say that these two reference axes must have different directions since they imply different concepts. That is, they must be linearly independent. They must have the quality of independence.

10.- REPRESENTATION OF THE RIGHT TRIANGLE WITH THE EXPRESSION OF ITS ROUTES BETWEEN ITS POINTS

The following figure presents the aforementioned three points and their routes between them. This triangle will be used to calculate the relationships that exist between the paths of the light and that of a mobile observer of the event.

Figure 2

Point (E) is where the event has appeared.

We interpret the vertical leg as the equivalent of the route of the EXTENSION of the event. We indicate it as (c.tp), being (c) the speed of light and calling (tp) Proper Time of the Extension.

We represent the end of the Extension with the point (F)

The horizontal leg serves to indicate the path and direction of a mobile body that moves at a uniform and rectilinear speed (v) from point (F) to point (O). We could consider it to be the body of the “observer.”

The hypotenuse of this triangle represents the path of the light ray that the observer has to perceive to SEE the appearance and development of the event. We write its travel time as (tr).

11.- WHY DO WE PLACE THE EXTENSION ON THE VERTICAL CATHETUS?

We already said that the two legs had to be linearly independent. Now we can ask ourselves why we put the Extension of the event as a length on the vertical leg and call it (tp). The answer is that this value represents the time in which an observer located at the end point (F) would be contemplating the entire development of the Extension. And so, in this way we capture an evaluation criterion of the Extension in a sketch.

12.- RELATIONSHIP BETWEEN THE TIME (tp) OF THE EXTENSION OF THE EVENT AND THE DISPLACEMENT TIME (td) OF THE OBSERVER

We have developed a mathematical procedure that allows us to value the time (tp) of the EXTENSION as a function of the Travel Time (td) required by the observer of the event to travel the itinerary described by the points (F-O).
Placing the EXTENSION of the event in the vertical leg of the triangle, valuing it as (tp) and valuing the travel time (td) that exists between the observation point (O) and the aforementioned vertical leg, we express the relationship between them as follows:

the expression:

is the so-called LORENTZ FACTOR, where (c) is the speed of light and (v) the speed of a Mobile body.

(NOTE: The mathematical development to obtain this equation is in the Second Part of this essay)

13.- THE LORENTZ FACTOR AS A TRANSFORMATION FACTOR OF THE DISPLACEMENT TIME (Ttd) IN MEASUREMENT OF THE EXTENSION (tp) OF THE EVENT.

To justify that the Lorentz Factor allows us to transform the value of the Travel Time (td) on the horizontal leg of the triangle to the observation point (O), into units of the Own Time (tp) of the event, that is, its EXTENSION, we will observe the formula given above from which we can deduce the following:

With which we can affirm that the Lorentz Factor is equivalent to valuing (td) in units (tp). It is a transforming factor that allows us to evaluate movements made at speeds (v) and transform them into speeds (c).

14.- EXPRESSION OF THE DISTANCES IN TIME USED IN RUNNING

Expressing the distances in times spent traveling them will allow us to consider only one of the transformation formulas set forth in the aforementioned book by A. Einstein.

We can express the distance between two points as the TIME taken to travel between these two points at a certain speed. This speed can be that of a moving body (v) or that of light (c).

Since we can consider the speed of light (c) constant, we can take it as a measure to evaluate distances and measure these distances in units of the speed of light (uvl).

In the following figure we can see that the distance between the observation point (O) and its mobile reference axes (K'), which has the observer as a reference, can be quantified by:

(X – v.(td))

Figure 3

From what we have mentioned, we can also express this distance in time spent traveling it (T), at a speed (v).

So we establish the equivalence: (X-v.t)≡(T)

15.- THE FORMULA FOR THE TRANSFORMATION OF SPACE GIVEN BY A. EINSTEIN IMPLICITLY CONTAINS THE EXPRESSION OF THE TWO PHYSICAL PHENOMENA THAT WE HAD INDICATED.

The fact that A. Einstein's space transformation formula does not fulfill the purpose that he assigns to it, this does not mean that its expression
implicitly contains the two physical phenomena to be considered.

Let us note that the numerator of the formula is: (X-v.t) which takes into account the physical phenomenon of displacement. We can verify this in Fig. 3.

Regarding the denominator of the aforementioned formula, we propose the following:

As we had explained, if

is equivalent to allowing the (td) to be valued in units (tp) and since (X-v.t) is equivalent to (td), we can deduce that: (X-v.t) is valued :

in units (tp). That is, in the Extension of the event.

Let it be clear that it allows us to SEE the Extension of the event. DO NOT transform the event.

16.- ANOTHER FORMULA TO ASSESS THE VISION OF THE EXTENSION OF AN EVENT FROM A MOBILE PLATFORM

In the previous issue we have seen that the formula for the transformation of space that A. Einstein gives us, although it does not fit the purpose that he proposes, we could use it with a theoretical approach to measure the extension (tp) of a event.

For theoretical purposes we can also give another expression that allows us to obtain (tp) as a function of the travel time (td) necessary to cover the distance between points (F) and (O).

Please note that this expression is obtained by solving for variables in the equation expressed in Point 12.

17.- WHY DO WE CALL THE FORMULA FOR THE TRANSFORMATION OF SPACE THE FORMULA FOR THE TRANSFORMATION OF THE VISION OF THE EXTENSION OF AN EVENT?

The name “vision transformation formula”
the extension of an event” has suggested to us when investigating the construction and possible use of this formula. So the reader can call it whatever he wants.

We have called it this way because of the following:

We can make a composition of figures 1 and 2 by superimposing them one on top of the other so that it globally represents the graphic expression of the aforementioned formula which, as we had commented, is the expression of the two physical phenomena.

In the following figure we can see that both the variables that imply the transfer of the coordinate axes appear, as well as the variables related to the vision of the event from a mobile observation point. That is, the variables corresponding to the right triangle.

Figure 4

If we consider that there is no movement and that the observer is fixed at the point (O), this observer WOULD SEE the Extension of the event located on the axis (K) and with a dimension equal to (E – F). But, if we now consider that the observer is moving and his reference coordinates are (K'), the VISION of the aforementioned event on these coordinates will have a dimension: (e – f). So we can say that the VISION of the event has BEEN TRANSFORMED. And this dimension of Extension is what the observer must operate with.

18.- IS THE RELATIONSHIP td/(tp) MAINTAINED WHEN THE MOBILE REFERENCE SYSTEM MOVES?

The doubt might arise if with this displacement of coordinates.

The relationship remains constant: td/tp, which allows us to measure the value of the Extension of the event. Using Geometry we can say yes, applying Thales' Theorem.

(NOTE: See the geometric explanation of Thales' Theorem in the second part of this study)

SECOND PART

This second part serves to expose the mathematical approaches and ideas that support the criteria that have been used in the first part, for the construction of the aforementioned formulas.

1.- CONDITIONS OF VALIDITY FOR THE VIEW OF THE EXTENSION OF AN EVENT FROM A MOBILE OBSERVATION POINT. SYNCHRONIZATION CONDITIONS.

Let's look at Figure 2. At a given instant it happens that: at point (E) in space an event appears and at this same instant the possible observer of this event is at point (F) in space.

From this initial instant begins the path of the light ray that carries the image of the event and the path of the observer who has to detect said event. Calling (tr) the time spent in the ray path and (td) the observer's path time, as the two paths must coincide at the observation point (O), we will impose as a synchronization condition:

(tr) = (td)

This is the condition that we will impose in the calculations that we will carry out below.

2.- MATHEMATICAL DEDUCTION OF THE RELATIONSHIP BETWEEN THE
OWN TIME OF THE EXTENSION OF THE EVENT AND THE TRAVEL TIME TO THE PLACE OF OBSERVATION

To relate the Proper Time (tp) of the Extension of the event, with the Displacement Time (td) we will apply the Pythagorean Theorem to the right triangle that we gave as a reference.

Requiring compliance with the Synchronization Condition:

(tr) = (td)

It allows us to replace (tr) with (td) with what we obtain:

Grouping terms we have:

We can transform the denominator in the following way:

Eliminating (c), gives as result

3.- DEMONSTRATION THAT BY MOVING THE VISION OF THE EXTENSION ON THE MOBILE REFERENCE SYSTEM, THE RELATIONSHIP BETWEEN THE (td) AND THE (tp) IS MAINTAINED.

To demonstrate this fulfillment we must remember Thales' Theorem. We can say that in a right triangle the proportionality relationship between the path of the horizontal leg and the vertical leg is fulfilled.

Let us remember that in the vertical leg we will represent the Extension (tp) of the Event and in the horizontal leg the travel time of the observer.

The following figure aims to demonstrate the validity of this theorem, by observing that the aforementioned proportions are maintained

Figure 5

4.- DEMONSTRATION THAT THE SECOND FACTOR OF THE NUMERATOR OF THE TIME FORMULA CAN BE TRANSLATED AS A TIME

When exposing the formula for the transformation of time we said that the expression: (v×X)/c² is nothing more than the expression of a “time”. 

Let's prove this statement.

In the VISION of an event, which we use a mobile Reference System (SRM) with respect to a Fixed Reference System (SRF), it must be taken into account that we use two types of speeds of a completely different nature. Let us remember that it is about: (v) and (c). 

We must homologate these two concepts if we want to incorporate them in the execution of the same physical phenomenon. We use the speed of light (c) as measurement pattern. That is, the 300,000 km/sec. as a unit of speed.

To make the aforementioned conversions we must take into account the following criteria to follow:

All lengths will be quantified using: “light speed units” (uvl).

This means that: the (uvl) are those that would be consumed to move between two certain reference points. For example, we can write: x = k (uvl) meaning that a certain length (x) is found, or would require k (uvl) to reach it.

A relationship such as: (v/c) assigns a fraction of (uvl) to a given velocity (v), since (c) is a fixed quantity taken as a unit, while (v) is the relative velocity between Inertial Reference Systems, different value in each specific case.

To quantify a length (l) we will apply the expression: l = x.( v /c)

This expression answers the question: A length (x) that has been traveled at speed (v) is equivalent to what length (l) if the speed were that of light (c)?

To obtain the travel time (td) of a Mobile Reference System (MRS) on the axis (X), operating with (uvl), we must divide the space (l) by the speed of light (c).
I mean:

(td) = (l) / (c) 

and since 

l = x.( v /c)

we obtain: 

(td) = (l) / (c) = ( x).(v / c) / (c) = ((x).(v))/c²