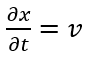(Intellectual Property Registry B-1221-21)
PRESENTATION
In our book titled; "Theory of relativity.
Criticism of a nonsense analyzed in seven installments ”, we are dedicated to criticizing
the different fallacies that appear written in the Theory of Relativity. Now,
we will dedicate ourselves to investigating some aspects of this Theory that
may remain somewhat obscure. With this introduction we want to differentiate
what was a criticism of some postulates, what is now about. It is a research
work by the same author of the aforementioned criticism.
In one of the fascicles of the aforementioned book we
quoted "the enigmatic Lorentz Factor", indicating with this
expression his contribution to the fallacy of "time dilation" without
relying on any logical criterion. Consider that, according to the story, these
mathematical expressions were obtained empirically. Now we will do the
"anatomy" to this Factor to investigate the mathematical function
that it fulfills. In the end we will show that the Lorentz Transformation
Formulas show that there is a ELONGATION of the viewing time of the Space and
Time variables of a physical phenomenon, and we will discard the fallacy of
TIME DILATION.
ONE OF THE APPEARANCES OF THE LORENTZ
FACTOR
In the Theory of Relativity, one of its parts in which
the Lorentz Factor intervenes is in the Transformation Formulas. Remember that
the expression of this factor (f) is
where (c) is the speed of light and (v) the speed
corresponding to a mobile.
We will dedicate ourselves to studying the function
that this mathematical expression fulfills, but first we will comment something
about the well-known Lorentz Transformation Formulas
To introduce ourselves to the subject of the formulas
of Lorentz Transformations, we quote the following.
In the book “On the theory of special and general
relativity” by A. Einstein, on page 32 (Edition “Alianza Editorial”), he
describes the form and usefulness of the formulas called the Lorentz
Transformations, as follows :
"Given the quantities (x, y, z, t) of
an event with respect to (k), what are the values (x`, y`, z´, t´) of the
same event with respect to (k´)?”
The relations must be chosen in such a way that they
satisfy the laws of propagation of light in a vacuum for one and the same ray
of light (and also for any ray of light) with respect to (K) and (K´). "
And he goes on to say:
"The problem is solved by the equations"
Space Formula
Figure 1

Time Formula
Figure 2

And, on this same page of the aforementioned book, the
following coordinate system (k) and (K´) is drawn
Figure 3

The variable (v) means the relative speed that the
system (K´) has with respect to the system (K)
The explanation that appears in the aforementioned
book, together with the previous drawing, helps little to understand the
purpose and way of using the aforementioned formulas.
The designation of the coordinate axis (X) can be
confused with the value of the variable (x) to be transformed. It uses three
coordinate axes when, as we will see later, only two coordinate axes will be
needed. Due to this difficulty of interpretation, we have chosen to create our
own design to analyze the mathematical structure of the Formulas of the Lorentz
Transformations
ANALYSIS OF THE VISION OF THE PHENOMENON
OF THE TRANSFORMATION OF THE VARIABLES OF AN EVENT.
First, we present some definitions that we will use in
our study.
We will call the physical phenomenon that we want to
observe EVENT and we will represent it by (E)
We will use Cartesian coordinates (X, Y) to place the
(E) in sidereal space. We must consider that we are dealing with RELATIVE
MMOVEMENTS, so we must consider a Fixed Reference System (SRF) and a Mobile
Reference System (SRM) regarding this (SRF)
We will call the duration or amplitude of the
variables Space (e) and Time (t) corresponding to (E) EXTENSIONS.
We will call the magnitude of the Extensions Own Time
and we will represent it with the variable (tp).
Regarding the vision of the physical phenomenon we say
the following:
In the vision of the phenomenon of the transformation
of the variables of an event, we will distinguish two parts.
FIRST PART
In the first part we will consider the TRANSFER of the
coordinate axes and the result of this transfer that affects the figures of the
variables Space (e) and Time (t) of the event.
In the following figure the observer VIEWS this
transfer.
Figure 4

This observer can evaluate the new value (x´) that the variable (X) had before the transfer, according to the expression:

The magnitudes of Space (e) and Time (t) of a physical phenomenon (E) are recorded as its length in the coordinate: x. We say that it is your Extension (X).
This Extension is the one that is transformed (or crossed over) when moving the coordinates.
These variables (X) will be the values of the Event Extension
Later we will see that these expressions of (X) will be identified as the Displacement Time
(td) of the coordinates, and that the Extensions will be identified with the Proper Time (tp) of this Event.
To carry out the evaluation of the result of the previous expression, it would be necessary:
Place the Event (E) in a certain position in sidereal space determined by the Cartesian coordinates (K).
Know the distance between the axes (K) and (K´) that would be calculated knowing the speed (v) and the time (t) of the transfer.
Observe the reader that the previous expression is the one that appears in the numerator of the Space Transformation Formula and, as we will see later, it also corresponds to the Time Transformation Formula.
SECOND PART
In the First Part we have considered that the
coordinate axes are already located in their place of observation. The TRANSFER
was already done and therefore it was a STATIC VISION. It is a photograph of an
event.
We are now going to consider a DYNAMIC VISION. It is
about wanting to observe the value of the Event Extensions (E) while the
location axis of the (E) is moving. It is moving. (Bear in mind that we are
dealing with RELATIVE MOVEMENTS).
This question enters fully into the study of the
Lorentz Factor that, as we can see, appears in the denominator of the
Transformation Formulas.
We will use new graphics to justify the approach of
the DYNAMIC VISION of Own Time (tp) corresponding to the Extension of an Event
(E)
CONDITIONS
OF SYNCHRONIZATION OF THE VISION OF THE EVENT IMAGE.-
We now begin the explanation of a topic that involves
the denominator presented by the two Transformation Formulas. We will see that
in it we will include the Lorentz Factor.
To analyze the simultaneous concepts of MOVEMENT and
OBSERVATION, we draw the following figure. We will call it: operational scheme.
Figure 5

In a certain position in sidereal space, a physical
phenomenon is located to which we want to quantify the magnitude of from your variable:
"space". Let us remember that: we will identify the physical
phenomenon as an EVENT (E). The magnitude of (x) we will call its EXTENSION. In
this operating diagram, we will identify the Extension as the Proper Time (tp)
of (E) and we will represent it on the (Y) axis of the drawing. We value the
magnitude of the Extension as (c.tp), where (c) is the speed of light and we
represent it in zic-zac as if it were a ray.
The aim is to observe the Extension of (E) from the
point (F) represented in the diagram. A
fixed observer, located at the origin of the coordinate axes (X, Y), could
observe the entire amplitude (c.tp) of the Extension space (e) or time (t) of
the Event (E)
For this to happen from another point in sidereal
space, it will be necessary for the DISPLACEMENT time (td) that the observer
will have taken to get to that point, be equal to the travel time (tr) of the
IMAGE of the Extension. Namely:
(td) = (tr)
so that the observer is not delayed or ahead of the
arrival of the information at the observation point.
We will call this equality "First Synchronization
Condition". This Travel Time (tr) as well as the (tp) we have drawn in
Zic-zac for traveling at the speed of light (c).
(NOTE: In the case of two Inertial Reference Systems
(SRI) we could also refer to the differential calculus. We would argue that the
Mobile Reference System moves in such a way that a travel time differential δtd
corresponds to a travel time differential δtr of the electromagnetic wave)
A second synchronization condition is that the time
elapsed during the displacement (td) is equal to the Extension (tp) of the
Event. Namely:
(td) = (tp)
so that the observer can contemplate from the point of
observation, the entire Extension.
(NOTE: We can justify the elongated shape of figure 5,
corresponding to a right triangle, as follows:
If (tp) = (td) and as c >> v =>
c. (Tp)> v. (Td)
which makes us think that if the right triangle were
equilateral, the speed (v) should be equal to (c) and it would be another topic
of analysis)
THE LORENTZ FACTOR.- A MATHEMATICAL
EXPRESSION THAT APPEARS IN TRANSFORMATION FORMULAS
We will study how we can RELATE the Proper Time (tp)
of the Extensions, with the Displacement Time (td) to the observation point.
For this we will observe Figure 5 and proceed to develop the calculations, applying
the Pythagorean Theorem

Demanding compliance with the First Synchronization
Condition
(td) = (tr)
allows us to make the substitution of (tr) for (td)
with what we obtain:

Grouping terms we have:

We can transform the denominator as follows:

Eliminating (c), results in

To the expression

it
is known as Lorentz factor.
It allows us to relate the Proper Time (tp) of the
Event with the Displacement Time (td) of the observer. Put together the
concepts we had talked about: Position and Movement.
THE LORENZ FACTOR AS A UNIT OF MEASUREMENT
OF THE OWN TIME OF THE VARIABLES SPACE (e) AND TIME (t)
To deduce how we can quantify the Proper Time (tp),
corresponding to the IMAGE of the Extension of a variable (x) due to the
MOVEMENT, from the Displacement Time (td) that the coordinates (K ') have
traveled, we do the following reasoning:
We start the equivalence relation that we had found:

From here we can deduce
another equivalence relation with the Lorentz Factor:

The quotient: td / tp we
can say that it is a way to quantify the (td) in units (tp)
Therefore, the Lorentz Factor is a transforming or
correcting factor, which transforms the Displacement Time (td) into units of
Own Time (tp). Therefore, applying this factor to (td) we obtain:

In this way we have justified the existence of the
Lorentz Factor in the aforementioned formulas.
Note that in the FIRST PART we had given the
expression: x´ = X-v × t in which we justified that we could consider it as a
Displacement Timep (td).
We have yet to
clarify one issue.
Now we are talking about a displacement time (td). How
can we apply the Lorentz Factor in the Space Form, as the denominator of the
expression:
X-v × t so that he can value us the (tp)?
To clarify this concept we will say that until now we
have been talking about TRAVELS of the coordinates (K´), and this is what the
previous expression shows, but now we enter into evaluating DISTANCES.
In this new approach to assessing Distances, we use
the speed of light. As we will see below, these distances will be valued in units
of the speed of light (u.v.l.)
This expression represents a travel time valued in
these units.
We believe that the time has come to talk about the
expression:

that appears in the numerator of the Formula of Time.
SPEED CORRECTIVE FACTOR.- DISPLACEMENT
TIME MEASUREMENT (td).
In the perception of the image of an event between two
Inertial Reference Systems with a velocity (v) between them, we must bear in
mind that we are using two completely different types of velocities in terms of
nature and orders of magnitude. They are two different Physical Magnitudes. We
can say that the relative speed (v) between the (MRS) and the (FRS) is between
masses while the information transmission speed corresponds to an
electromagnetic wave with a speed of light (c) well above or above the least
very different from the velocity (v). It is obvious that, although these are
two expressions that are related to "speed", they are different. They
do not have the same physical nature. They should be treated as different. The
speed of light (c) is always the same. It is inherent in itself. It is a
constant and with an order of magnitude infinitely greater than what is
supposed to be on the (X) axis. That is (v). We cannot compare or establish a
relationship between two lengths or two times that are measured using different
patterns of measuring speeds. They should be normalized so that they both use
the same type of pattern.
We use the speed of light (c) as a standard. That is,
the 300,000 kms / sec. as a unit of speed
To make the aforementioned conversions we must take
into account the following criteria to follow:
All lengths will be quantified using: "light
speed units" (uvl).
This means that: the (uvl) are those that would be
consumed to move between two certain reference points. For example, we can
write: x = k (uvl) referring to where a certain length (x) is found, or it
would require k (uvl) to reach it. (The "light unit" is a measure of
speed that is worth: 300,000 km / sec. That is, one (uvl) is equal to 300,000
km / sec.)
A relationship such as: (v / c) assigns a fraction of
(uvl) to a certain speed (v), since (c) is a fixed quantity that is taken as a
unit, while (v) is the relative speed between Los (SRI), different value in
each specific case.
To quantify a length (l) we will apply the expression:
l = x. (v / c)
This expression answers the question: A length (x)
that has been traveled at the speed (v) to what length (l) is it equivalent if
the speed were that of light (c)?
To obtain the displacement time (td) of a Mobile
Reference System (SRM) on the axis (X), operating with (uvl), we must divide
the space (l) by the speed of light (c).
I mean:
(td) =
(l) / (c) and since l = x. (v / c)
we get: (td) =
(l) / (c) = (x). (v / c) / (c) =
Expression that
appears in the numerator of the Formulla of the Transformation of Time and that
it is the expression of a time.
CONSTANCE OF THE RELATIONSHIP BETWEEN EL (td)
AND EL (tp). TALES THEOREM
To facilitate the interpretation of what we are going
to present we present the following figure
Figure 6

The drawing represents a certain position, in sidereal
space, of the coordinates (K´) after having traveled a certain space valued as
(td).
In this situation of the coordinates (K´) we can
apply, for example, the Space Formula to visualize the Extension of an Event
(E) located in the coordinates (K).
We ask ourselves now:
If the coordinates (K´) continue to move, will the
application of the Formula be valid for all the different situations that it
can reach?
The logical answer seems to be yes. However, we cannot
give this answer without endowing it with a certain scientific rigor.
To justify it we say the following:
We intend to show that the quotient: c = td / tp must
be a constant value (K) for any value of (td).
If we show that: td / tp = K for any point on the path
(td), then we can admit
tp = td / k
for all points along the coordinate path.
We carry out the proof using Thales' Theorem, the
fulfillment of which we illustrate with the following figure.
Figure 7

As agreed, in the vertical leg we will represent the
extension (tp) of the Event. This extension has a certain value for a certain
physical phenomenon to be observed. Placing the observation point at a certain
distance, when determining the value of the relationship:
td / tp, the same value is obtained: 1.70 whether you
start counting the displacement time (td) from the origin of coordinates, or if
you start counting the displacement from any point (P) intermediate between the
origin and the end of the route. In the case of the drawing, this point is 9.5
from the observation point.
It is evident that this condition of preserving the
values: td / tp is general. For a specific phenomenon, it is valid for its
constant value (tp) and possible variable values of (td).
ANALOGY OF THE TRANSFORMATIONS OF LORENTZ
WITH THE MENTAL EXPERIMENT OF THE TRAIN CAR
In this chapter we will remember what we explained in
our book: “Theory of Relativity. - Criticism of a nonsense analyzed in seven fascicles ”, regarding the “ Mental Experiment
of the Train Car ”. The purpose of this reminder is to establish an analogy
between this experiment and the Transformation Formulas that we have studied,
and from here draw the conclusion that we are facing a LENGTHENING OF THE
VISION OF A FACT OR CAUSE. It is not a DILATION OF TIME.
Let us remember that in the aforementioned book we
question the conclusions of this experiment and label it as the "genesis
of nonsense." We said that these were two different and simultaneous experiments.
This makes us realize that we have obtained a RELATIONSHIP between two physical
quantities from two different phenomena.
We transfer the drawing of that thought experiment:
Figure 8

In the left part of the drawing the phenomenon of the
reflection of the light beam in a mirror that is located on the roof of the
wagon is represented. The train car is stopped and the round trip time of the
reflection in the mirror recorded by the observer (O1) is really the Proper
Time (tp) of the physical phenomenon.
Another observer (O2) situated still on the embankment
would take a longer time (td) than the one observing (O1) due to the fact that
in the phenomenon of light reflection it also contemplates the displacement of
the mirror.
It is clear that these are two different trials.
In the explanation of the Transformation Formulas we
have mentioned the Proper Time (tp) of the Extension of the Event, which we can
associate with the (tp) of the phenomenon of the reflection of the light ray.
This interpretation is exposed in the left part of Figure 8. Let us remember
that the (tp) is inherent to the phenomenon. In the case of the train car, it
corresponds to the phenomenon of the reflection of light in the mirror. In the
case of Formulas, it corresponds to the assessment of the VISION phenomenon of
the Extension variable of an Event, observed at a given moment. This is the
photograph of the phenomenon. But it must also be taken into account that the
observation is made from a Mobile Reference System (SRM).
The following figure attempts to demonstrate our claim
Figure
9

The Proper Time (tp) of the physical phenomenon of the
reflection of the ray of light in the mirror is represented in the left part of
the drawing. With the wagon stopped.
In the right part of the drawing an observer appears
outside the car. He is fixed on the ground and observing the path of the light
beam while the wanderer is moving for a Displacement Time (td). It is evident
that different observation values of the phenomenon will be appreciated. It
will be obtained (td)> (tp). This is the interpretation that we must give to
the aforementioned Formula when considering the observation from a Moivil
Reference System (SRM).
THE FORMULAS INDICATE US THAT IT IS ABOUT:
A LENGTHENING OF THE VISION OF THE EXTENSIONS. IT IS NOT A TIME DILATION
Using the example of the train car thought experiment,
we will justify the EXTENSION of the VISION of the Extensions of an Event.
Let's see what the Formulas ask us to get answers:
Let us remember that we incorporate the Lorentz Factor
into the formulas when we contemplate a DYNAMIC VISION of the phenomenon to be
observed.
In the first place we were talking about a STATIC
VISION, which is what happened when the references changed due to the
displacement of the coordinates. It is equivalent to Own Time
(tp) of the process, which records the operator who
goes inside the train station.
Another experiment is the DYNAMIC VISION that we
consider that the observer contemplates the movement of the experiment. It does
not move with it. It has come out of it. In this circumstance, your VISION
measurement of the Event Extension duration will be longer since you are adding
the time it takes for the process to travel to the point where the end of the
observation is considered. We can see the analogy that we are establishing with
the observer who is fixed on the ground in the example of the thought
experiment of the train car.
This increase in observation time is reflected in the
formula by incorporating the Lorentz Factor.
First, let's
note that:

Recall that the expression of the numerator of the
Space Formula is: (X-v × t). Therefore, the complete expression of the formula:

indicates that that initial value has been increased
and this is due to considering the displacement movement that it is being
produced.
![]()

 On the other hand, the magnitude of a force (F) can also be estimated using other physical units. We can assess it by intervening the acceleration (a) that it prints on the mass (m) on which it is constantly acting. I mean:
F = m.a
We also know that:
On the other hand, the magnitude of a force (F) can also be estimated using other physical units. We can assess it by intervening the acceleration (a) that it prints on the mass (m) on which it is constantly acting. I mean:
F = m.a
We also know that:
 where (dv) is the speed increase that is being reached in each differential (dt) of the time that is passing. So we can write:
where (dv) is the speed increase that is being reached in each differential (dt) of the time that is passing. So we can write:
 The expression of the Work done is expressed as:
The expression of the Work done is expressed as: