CONTRADICTIONS AND ERRORS OF A. EINSTEIN IN HIS THEORY OF RELATIVITY

PRESENTATION

In this essay we criticize the Theory of Special Relativity and the Theory of General Relativity of A. Einstein

The study is divided into the following three parts:

A.- Bases established by A. Einstein to argue his theory of special relativity

B.- Contradictions of A. Einstein in his theory of special relativity, with respect to the bases that he had established in another book

C.- Contradictions of A. Einstein in his theory of general relativity.- His error in the principle of equivalence

The texts transcribed from A. Einstein's books will be written between quotation marks and in italics.


A.- BASIS ESTABLISHED BY A. EINSTEIN TO ARGUMENT HIS THEORY OF SPECIAL RELATIVITY

We discuss the basic principles that A. Einstein uses to argue his Theory of Special Relativity and that later, we will see that he contradicts them.


1.-INERTIAL REFERENCE SYSTEMS

We remind the reader of a basic concept that appears in the theory of relative motions.

Let us imagine in sidereal space a body that is moving relative to another with a certain uniform and rectilinear speed. By definition, we will say that an Inertial Reference System (SRI) has been established between these bodies.

We will designate the body that we assume moves with respect to the other with the name Mobile Reference System (MRS). The other body, which we will take as a reference or as the origin of the movement, will be designated as the Fixed Reference System (SRF).

A further step will be to consider that these “bodies” are containers of physical phenomena, with their corresponding laws that govern them.


2.- THE FIRST PRINCIPLE OF RELATIVITY.- GALILEO'S PRINCIPLE.

In order to observe the contradictions that the Theory of General Relativity presents, by attempting to include accelerated movements, we must begin our essay by stating the Principle of Relativity.

Taken from A. Einstein's book titled: “On the theory of special and general relativity” (Page 18) the first Principle of relativity says:

“If a (SRM) moves with respect to a (SRF) then natural phenomena occur with respect to the (SRM) according to the same general laws as with respect to the (SRF).

Just as a comment we cite as an example that: Galileo Galilei already announced this principle in 1632, using the mental experiment of the hold of a ship in uniform and rectilinear motion)

3. WHAT DID A. EINSTEIN INTEND TO JUSTIFY WITH HIS THEORY OF RELATIVITY?

Knowing the concepts of relative movements and what is understood by inertial reference systems, we will be in a position to understand the answer to the question: what do we think A. Einstein intended to justify in his theory of relativity?

We find the answer in his book: “The meaning of relativity” by A. Einstein (Page 38). There the author notes the validity of Inertial Reference Systems (IRS) to be able to examine and measure the laws of nature in the same way and with the same results in each of them. Using mathematical and non-physical terms, we could say that the (SRI) are reference coordinate systems with respect to others.

On the aforementioned page of that book the following explanation appears:

“…there are Cartesian coordinate systems, the so-called inertial, with respect to which the laws of Mechanics (more generally, the laws of Physics) have the simplest form. We can infer the validity of the following theorem: if K is an inertial system, any other system k', endowed with uniform motion and without rotation with respect to K, is also an inertial system and the laws of nature are consistent with each other when use any inertial system to express them. We will call this statement the “principle of special relativity.”

In short: in an Inertial Reference System, the same natural phenomena develop and are conditioned by the same laws.


B.- CONTRADICTIONS OF A. EINSTEIN IN HIS THEORY OF SPECIAL RELATIVITY WITH RESPECT TO THE FOUNDATIONS HE HAD ESTABLISHED IN ANOTHER BOOK

Everything that we have exposed in “part A” of this essay and preached by A. Einstein himself, we will now see what he denies. It enters the dark tunnel of confusing the use of the verb SEE with the verb BE, an error that we have already commented on in our previous essays.

This confusion consists of the fact that, just because there is a relative movement between a Mobile Reference System (SRM) with respect to a Fixed Reference System (SRF), natural phenomena and their laws are modified. And this is the confusion that we have exposed.

The aforementioned Physicist says that physical phenomena and their laws ARE different when in reality, to be consistent with his previous statements, he should understand that they LOOK different. The statement that they ARE different contradicts their previous arguments that we have presented.

Next, we will comment on some of our previous essays in which we already warned of the error of confusing the use of the verb SEE with the verb BE.

(NOTE: The reader can consult in our Blog the topics that we are going to briefly summarize. All the topics that we criticize appear in A. Einstein's book titled “On the theory of special and general relativity)

1.- THE LONGATION OF THE REFLECTION TIME OF A RAY OF LIGHT IN THE MIRROR OF A TRAIN CAR CIRCULATING AT A CONSTANT AND STRAIGHT SPEED.

We show that the (SRF) VE extends the duration of the longest light ray. But it is not that time has dilated as some physics books argue. You SEE the extension of time at the speed of light, added by the speed of the train itself. “Added” but not dilated.


2.- THE SHORTENING OF THE MEASURING BAR

In one of the paragraphs of the aforementioned book, it presents a length measuring bar on top of a mobile train car. And it says that the bar is shortened with respect to (SRF), simply because of its relative movement. By considering the verb BE you come to admit the nonsense that the measuring bar has become shorter. The bar has not been shortened, it LOOKS shorter because the end of the bar travels on the car against the vision of the (SRF)


3.- THE RELATIVITY OF SIMULTANEOUSNESS

In another paragraph of the book he raises the “relativity of simultaneity.” Due to the same confusion already mentioned, he manages to admit the nonsense, which we ironically call “the miracle of transmutation.” The matter has changed state.

(Note: In one of our previous essays we explained where the trap lies to justify such an error of trying to destroy the simultaneity of two events and consider them different)


4.- THE PARADOX OF THE TWIN BROTHERS

The same books that deal with the subject of the theory of special relativity already classify as a “paradox” that the astronaut twin brother, when he returns to Earth, finds his twin brother older.

Confusing the verb SEE with the verb BE turns the story into a science fiction story


5.- THE PHASE LAG IN CLOCKS WITH RELATIVE MOVEMENTS

Another issue with the same justification that we have been exposing is found in the fictitious phase difference between clocks with relative movements. We could combine this nonsense with that of the paradox of the twin brothers. To justify the nonsense, dubious publications appear that try to validate it, mentioning experiments of dubious authorship and accuracy.


6.- LORENTZ'S TRANSFORMATIONS

These transformations of the variables of a formula do not occur as described by A. Einstein in his aforementioned book. The variables involved are not transformed. We demonstrate in one of our essays what they consist of, how to obtain them and what they LOOK like.


C.- CONTRADICTIONS OF A. EINTEIN IN HIS THEORY OF GENERAL RELATIVITY.- HIS ERROR IN THE PRINCIPLE OF EQUIVALENCE

This third part of this essay will serve to criticize the error of wanting to include accelerated movements in the fulfillment of physical phenomena and their corresponding laws.

In this third part we will distinguish two themes. One topic is focused on demonstrating non-compliance with the laws of natural phenomena if we intend to use accelerated speeds in relative movements. We dedicated the other topic to speculating about the possible erroneous arguments that the aforementioned Physicist used to reach such confusion of ideas.


1.- SUMMARY OF THE ELEVATOR MENTAL EXPERIMENT

With the thought experiment of the elevator, A. Einstein intends to justify the extension of his theory of relativity to reference systems that move with accelerated movements. We will see that this is a chimera

(NOTE: In our essay titled: “Theory of general relativity. - A science fiction story” the reader can read the entire elevator thought experiment” that we have transcribed from A. Einstein's book: “On the theory of relativity special and general)

A summary of the approach to this thought experiment, as described by A. Einstein, is as follows:

A box, which we will identify as an elevator and place in sidereal space, is pulled upwards, with a uniformly accelerated speed: ∆(v), by a rope attached to the roof of the box. Inside this elevator there is a person who is a passenger. This person notices the pressure exerted by the elevator floor because the traction force exerted by the aforementioned rope is transmitted throughout the elevator casing to the elevator floor.

The following figure is intended to signify the elevator thought experiment.

2.- CONCLUSIONS DRAWN BY A.EINSTEIN FROM HIS MENTAL ELEVATOR EXPERIMENT 

If we read the aforementioned mental experiment in its entirety we can make the following summary: Since the accelerated movement that the rope gives to the elevator causes in the person who is inside it a SENSATION equivalent to that caused by a gravitational field, this allows him to extend his theory to accelerated relative movements. We transcribe some final pieces of his conclusions: “But how does the man in the box judge the process?”… … ”Based on his knowledge of the gravitational field, as we discussed in the last section, the man will conclude that he is, along with the box, within a fairly constant gravitational field.” ..."So we have good reasons to extend the principle of relativity to reference bodies that accelerate with respect to each other, and thus a powerful argument has been won in favor of a postulate of generalized relativity." With these statements it seems that everything would fit to accept the expansion of the aforementioned theory. However, a deeper analysis will show us that this approach has very little consistency. It is a fallacy and the laws subject to natural phenomena could not be fulfilled as we discussed in our previous chapters.

3.- AN INCORRECT INTERPRETATION OF THE CONCEPT EQUIVALENCE

Reading the latest statements that A. Einstein makes in the elevator thought experiment, we wonder if we can call EQUIVALENTS the traction force generated by the elevator rope through the casing to the floor of the elevator and a hypothetical gravitational field. We believe that in the sense that A. Einstein uses the similarity of the aforementioned effects, the word EQUIVALENT is not correct. The aforementioned Physicist uses this similarity to indicate that the two CAUSES produce the same EFFECT. They produce a sensation of pressure on the feet of the traveler who is inside the elevator. We say that the word EQUIVALENCE is not correct because its extension limits it to a single type of EFFECT. The equivalent word must be more demanding. It must require that ONE CAUSE can be replaced by another giving the same EFFECT or result. And this is what does not happen in the EQUIVALENCE that A. Einstein presents in the story of his elevator thought experiment. Admitting the meaning of EQUIVALENTS as he presents it, is as absurd as justifying that a pot with boiling water inside and an electric stove plugged into the outlet are EQUIVALENT, because the two utensils give off heat.


4.- THE CONFUSION OF A. EINTEIN.- THE WRONG EQUIVALENCE OF ONE FORCE FOR ANOTHER OF A DIFFERENT SIGN

Now we will try to find out what A. Einstein's confusion was that led him to preach an error.

He says that the traction force of the rope and the fictitious gravitational field are equivalent, because they make the same SENSATION perceived in the feet of the passenger in the elevator. However, he forgets that the important thing is to determine how the forces he says are involved ACT. And, if we take this into account, we must consider that two different types of force actually ACT and, therefore, we cannot speak of EQUIVALENCE.

We must consider that in the aforementioned experiment a Contact force and an Attraction force intervene. The Contact Force can be Traction or Push.

The following figure aims to expose the ACTIONS of these two types of forces:

We can transfer the performance of the two types of force: Traction Force and Attraction Force, to the elevator floor of the thought experiment.

The following drawing aims to simulate the elevator pulled by a rope that imposes a uniformly accelerated speed.

∆(v), and the forces that are said to act on the feet of the traveler inside it.

In the image we can see that the traction force exerted by the rope on the floor of the elevator through its casing and a hypothetical force of attraction due to a hypothetical gravitational field are not at all EQUIVALENT. Using terms from Physics, these forces are vectors of different signs and we cannot quantify them with the same value. Their EQUIVALENCE is not useful for us to exchange them in the formulas of the laws that govern natural phenomena.


5.- INCAPACITY OF REFERENCE SYSTEMS WITH ACCELERATED RELATIVE MOVEMENTS

Reference Systems with accelerated relative movements, unlike Inertial Reference Systems, cause displacements of the mass and, consequently, the laws of classical mechanics are not applicable.

As an example we can take that of a train car in a phase of its movement in which it is accelerating. Its uniform increase in speed: ∆(v) causes the mass (m) inside to move from the front wall of the car to its rear wall. At this point, the dough will be “stuck” to the front wall without being able to move.

This image can also serve to highlight that there is no EQUIVALENCE between the gravitational field that operates throughout the carriage and its contents, and the traction force caused by the engine of the train carriage, in a direction perpendicular to that caused by the previous force . The acting forces cause two different CAUSES. These are attachment to the ground and accelerated movement. Physically speaking, they are vectors that have different directions. They are linearly independent. Not EQUIUVALENT.

Continuing with accelerated movements we can also use as an example a pendulum anchored inside the car. If we assume that when the movement of the wagon begins, the ball of the pendulum is near the front wall of the wagon, as the speed accelerates, in the end the said ball will be near the rear wall of the wagon and from there it will no longer be able to move. . The law of the pendulum will not be fulfilled.

The following figure aims to expose this circumstance.

This tells us that accelerated movements do not allow include them within natural phenomena and the laws that govern them. A pendulum clock inside this accelerated car (SRM) could not indicate the passing time as a pendulum clock located in its response (SRF) would do.


6.- SPECULATION ABOUT A. EINSTEIN'S ERROR IN HIS PRINCIPLE OF EQUIVALENCE

With the understanding that we are going to express our own opinion, we are going to speculate regarding A. Einstein's error in trying to establish an EQUIVALENCE between a Traction Force and an Attraction Force corresponding to a fictitious gravitational field, and we propose the following:

In his book titled “On the Theory of Special and General Relativity,” the chapter in which he describes the elevator thought experiment begins with the following title:

“The equality between inertial mass and gravitational mass as an argument in favor of the postulate of general relativity”

This distinction between two types of dough that behave in the same way is the beginning that causes confusion.

In the aforementioned book he starts from the concept that a body has two types of mass. The inertial mass and the gravitational mass. After using a twisted tour of concepts and arguments, on page 60 of the book, he comes up with a formula, of dubious validity and without any type of demonstration, to try to justify that the quotient between the Inertial Mass and the Gravitational Mass is worth “1” , and from here he draws the conclusion:

“The Gravitational Mass and Inertial Mass of a body are equal”

Regarding this statement we make the following reasoning:

As he started from making the distinction between inertial mass and gravitational mass, by applying the “mysterious formula and saying that “they are equal” he is referring to the fact that they are numerically equal, but we must understand that he maintains the idea that there are two different types of mass.

In this statement we perceive that it rather refers to a numerical equality and NOT to “which is the same.” In other words, it does not refer to congenital equality or material identity, and this is his big mistake. He considers the existence of two types of dough.

We believe that: for all bodies there is only one type of mass. This mass behaves, or reacts, differently depending on the type of force to which it is subjected. The forces are the CAUSES and the behavior of the mass is the EFFECT. These forces are of two types and their BEHAVIOR on the mass is totally different. Let us remember that we classify them as: Force of Attraction and Force of Traction or contact.

In summary, we believe the following:

By considering that it is not forces but masses that act, it distorts the meaning of the experiment. By omitting the forces as operating factors in the experiment, it makes them equivalent to each other. That is, a Traction Force equivalent to a Force of Attraction and here is the error.

A. EINSTEIN'S ERRORS ANALYZED WITH LORENTZ'S TRANSFORMATION FORMULAS

PRESENTATION

Reading in A. Einstein's book entitled: “On the theory of special and general relativity” the topic of the Lorentz Transformation Formulas, some doubts have arisen. Having analyzed these doubts, we have seen that they come from two errors. These are the same errors that we already exposed in our previous essays, in which we denounced that through relative movements the author of the aforementioned book confused the verb SEE with the verb BE. And, thus, we ironically say that he preaches “the miracle of transmutation.”

We dedicate this essay to highlighting the aforementioned errors and to proposing a method of analysis to construct and interpret the aforementioned formulas. For better follow-up of this study, we have divided it into two parts. The second part is somewhat more theoretical than the first and some mathematical developments appear.

FIRST PART

In this first part we will propose and explain the steps to follow for the construction of the Lorentz Transformation Formulas. We will call these formulas: “Formulas of the VISION of the Extension of an event observed from a mobile platform”, in order to correct the distorted acceptance between the verbs: SEE and BE.

1.- AN EXPLANATION THAT APPEARS IN A BOOK BY A. EINSTEIN

In the book “On the theory of special and general relativity” by Einstein, on page 32 (Edition “Alianza Editorial”), he describes the form and usefulness of the formulas called Lorentz Transformations, as follows:

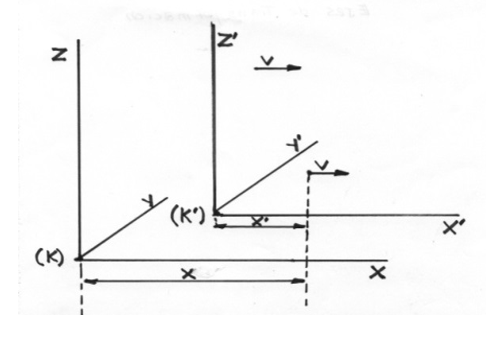
“Given the quantities (x,y,z,t) of an event with respect to (k), what are the values (x`,y`,z´,t´) of the same event with respect to (k´)?

The relations must be chosen in such a way that they satisfy the laws of light propagation in a vacuum for one and the same ray of light (and also for any ray of light) with respect to (K) and (K´).”

And he goes on to say:
“The problem is solved by the equations”
Space Formula

Formula of Time

And, on this same page of the aforementioned book, the following coordinate system (k) and (K) is drawn.

Figure 1

Later we will demonstrate that the expression: (v×X)/c² that appears in the time formula, translates as a time and that with the “space formula” there would be enough to make “theoretical” applications.

2.- WHERE DO WE FIND ERRORS IN THE EXPLANATION GIVED BY A. EINSTEIN IN THE LORENTZ TRANSFORMATION FORMULA?

The first error we found in the explanations given by the Physicist about the Formulas and Lorentz Transformations is the following:

When asking:

What are the values (x`,y`,z´,t´) of the same event with respect to (k´)?

We believe that you are thinking about “transformation” or “converting” rather than SEEING the event from a mobile platform regarding the event. We believe this is one of the errors. He falls back into the error that we have already commented on in previous of our essays. Through relative movements he confuses the verb SEE with the verb BE. In this way he prepares what we have called “the miracle of transmutation”. We say that he is thinking about the “transformation” since in the mental experiment of the bar for measuring lengths, subjected to a relative movement, he applies the formula for the transformation of space and preaches the nonsense of the shortening of the aforementioned bar. This error consists of believing in the “transformation” of matter.

The second mistake consists of wanting to apply the conclusions drawn in a mental experiment to a real-life physical experiment.

We wonder if the results obtained from a thought experiment can be applicable in real life.

We believe that the answer has to be negative. Precisely, the problem is reasoned by applying a mental experiment because it is not possible to apply a physical experiment. And, so far, it seems that it is a chimera to try to build a physical experiment that transcribes the results of a mental experiment. All this is aggravated if in the mental experiment the action of SEE has been confused with the verb BE.

In this essay we will see that the expression will appear.

In which (v) is the speed of a moving body and (c) is the speed of light. Even considering (v) one of the greatest speeds in our real world, for example the speed of a space rocket, its speed is so small with respect to that of light (c) that the quotient that appears within the radical of the expression that we have written would be an infinite value. That is why we say that, as we will see, it would be a chimera to transfer it to a physical experiment.

(NOTE: Do not confuse, as A. Einstein states, that the limit speed that can be reached is the speed of light. The reader can read the essay contained in our Blog, titled: “Theory of relativity. - It is possible that a particle can travel at a speed faster than light." Note that there we are talking about a particle and not a body endowed with movement.)

3.- WHAT DO WE UNDERSTAND BY THE DIMENSION OF AN EVENT?

We will understand the dimension of an event as its duration from its appearance until its extinction. We can value this duration in length or time. We will call this dimension EXTENSION of the event.

4.- WE ASKED, IN A THEORETICAL APPROACH, WHAT WOULD TRANSFORMATION FORMULAS BE USED FOR?

According to our approach we will say that its purpose would be: Assess the dimension of an event, which occurs in a certain position in space, by an observer who is moving at a constant and rectilinear speed (v) with respect to this event.

(NOTE: The reader should note that we are talking about a “theoretical” approach. At the end we will explain that this approach, using mathematical resources, could hardly be applied in our real life)

5.- FORMULA FOR THE TRANSFORMATION OF THE VISION OF THE EXTENSION OF AN EVENT

In order not to confuse with the erroneous purpose that Einstein intends to give to the Lorentz transformation formulas, in our analysis we will call them: Transformation formulas of the VISION of the Extension of an event. The reader should note that we highlight the verb SEE.

6.- ACTIONS IMPLIED IN THE TRANSFORMATION OF THE VISION OF THE EXTENSION OF AN EVENT

To build the “formula for the transformation of the VISION of the Extension of an event”, in our study we will consider three actions implicit in it. These actions are the following:

APPEAR the event; REMAIN your visibility; SEE your Extension.

7.- TWO PHYSICAL PHENOMENA TO CONSIDER

When constructing the transformation formula we must take into account that two physical phenomena overlap. One is the movement and displacement of the observer of the event at a speed (v). The other physical phenomenon is the VISION of the event, from the place where the observer has moved, and in which the speed of light is involved (c).

8.- A RIGHT TRIANGLE TO ANALYZE THE VISION OF THE EXTENSION OF AN EVENT FROM A MOBILE PLATFORM

To analyze the VISION of the Extension of an event from a mobile platform we will use a right-angled triangle.

We must define the situation of three points representative of: Appearance of the event (E); Completion of the Extension of the event (F) and Observation of the event (O). With these three
points we define a triangle

9.- WHY SHOULD THE TRIANGLE BE RECTANGLE?

To position the event and its observation position in space, we will consider the two legs of the triangle as coordinate axes. The legs of the triangle must be perpendicular to each other. This is so since:
On the horizontal axis we will give the meaning as the path of the movement and the speed (v), and on the vertical axis we will express the dimension of the Extension of the event. Without going into more specialized mathematical expressions, we only say that these two reference axes must have different directions since they imply different concepts. That is, they must be linearly independent. They must have the quality of independence.

10.- REPRESENTATION OF THE RIGHT TRIANGLE WITH THE EXPRESSION OF ITS ROUTES BETWEEN ITS POINTS

The following figure presents the aforementioned three points and their routes between them. This triangle will be used to calculate the relationships that exist between the paths of the light and that of a mobile observer of the event.

Figure 2

Point (E) is where the event has appeared.

We interpret the vertical leg as the equivalent of the route of the EXTENSION of the event. We indicate it as (c.tp), being (c) the speed of light and calling (tp) Proper Time of the Extension.

We represent the end of the Extension with the point (F)

The horizontal leg serves to indicate the path and direction of a mobile body that moves at a uniform and rectilinear speed (v) from point (F) to point (O). We could consider it to be the body of the “observer.”

The hypotenuse of this triangle represents the path of the light ray that the observer has to perceive to SEE the appearance and development of the event. We write its travel time as (tr).

11.- WHY DO WE PLACE THE EXTENSION ON THE VERTICAL CATHETUS?

We already said that the two legs had to be linearly independent. Now we can ask ourselves why we put the Extension of the event as a length on the vertical leg and call it (tp). The answer is that this value represents the time in which an observer located at the end point (F) would be contemplating the entire development of the Extension. And so, in this way we capture an evaluation criterion of the Extension in a sketch.

12.- RELATIONSHIP BETWEEN THE TIME (tp) OF THE EXTENSION OF THE EVENT AND THE DISPLACEMENT TIME (td) OF THE OBSERVER

We have developed a mathematical procedure that allows us to value the time (tp) of the EXTENSION as a function of the Travel Time (td) required by the observer of the event to travel the itinerary described by the points (F-O).
Placing the EXTENSION of the event in the vertical leg of the triangle, valuing it as (tp) and valuing the travel time (td) that exists between the observation point (O) and the aforementioned vertical leg, we express the relationship between them as follows:

the expression:

is the so-called LORENTZ FACTOR, where (c) is the speed of light and (v) the speed of a Mobile body.

(NOTE: The mathematical development to obtain this equation is in the Second Part of this essay)

13.- THE LORENTZ FACTOR AS A TRANSFORMATION FACTOR OF THE DISPLACEMENT TIME (Ttd) IN MEASUREMENT OF THE EXTENSION (tp) OF THE EVENT.

To justify that the Lorentz Factor allows us to transform the value of the Travel Time (td) on the horizontal leg of the triangle to the observation point (O), into units of the Own Time (tp) of the event, that is, its EXTENSION, we will observe the formula given above from which we can deduce the following:

With which we can affirm that the Lorentz Factor is equivalent to valuing (td) in units (tp). It is a transforming factor that allows us to evaluate movements made at speeds (v) and transform them into speeds (c).

14.- EXPRESSION OF THE DISTANCES IN TIME USED IN RUNNING

Expressing the distances in times spent traveling them will allow us to consider only one of the transformation formulas set forth in the aforementioned book by A. Einstein.

We can express the distance between two points as the TIME taken to travel between these two points at a certain speed. This speed can be that of a moving body (v) or that of light (c).

Since we can consider the speed of light (c) constant, we can take it as a measure to evaluate distances and measure these distances in units of the speed of light (uvl).

In the following figure we can see that the distance between the observation point (O) and its mobile reference axes (K'), which has the observer as a reference, can be quantified by:

(X – v.(td))

Figure 3

From what we have mentioned, we can also express this distance in time spent traveling it (T), at a speed (v).

So we establish the equivalence: (X-v.t)≡(T)

15.- THE FORMULA FOR THE TRANSFORMATION OF SPACE GIVEN BY A. EINSTEIN IMPLICITLY CONTAINS THE EXPRESSION OF THE TWO PHYSICAL PHENOMENA THAT WE HAD INDICATED.

The fact that A. Einstein's space transformation formula does not fulfill the purpose that he assigns to it, this does not mean that its expression
implicitly contains the two physical phenomena to be considered.

Let us note that the numerator of the formula is: (X-v.t) which takes into account the physical phenomenon of displacement. We can verify this in Fig. 3.

Regarding the denominator of the aforementioned formula, we propose the following:

As we had explained, if

is equivalent to allowing the (td) to be valued in units (tp) and since (X-v.t) is equivalent to (td), we can deduce that: (X-v.t) is valued :

in units (tp). That is, in the Extension of the event.

Let it be clear that it allows us to SEE the Extension of the event. DO NOT transform the event.

16.- ANOTHER FORMULA TO ASSESS THE VISION OF THE EXTENSION OF AN EVENT FROM A MOBILE PLATFORM

In the previous issue we have seen that the formula for the transformation of space that A. Einstein gives us, although it does not fit the purpose that he proposes, we could use it with a theoretical approach to measure the extension (tp) of a event.

For theoretical purposes we can also give another expression that allows us to obtain (tp) as a function of the travel time (td) necessary to cover the distance between points (F) and (O).

Please note that this expression is obtained by solving for variables in the equation expressed in Point 12.

17.- WHY DO WE CALL THE FORMULA FOR THE TRANSFORMATION OF SPACE THE FORMULA FOR THE TRANSFORMATION OF THE VISION OF THE EXTENSION OF AN EVENT?

The name “vision transformation formula”
the extension of an event” has suggested to us when investigating the construction and possible use of this formula. So the reader can call it whatever he wants.

We have called it this way because of the following:

We can make a composition of figures 1 and 2 by superimposing them one on top of the other so that it globally represents the graphic expression of the aforementioned formula which, as we had commented, is the expression of the two physical phenomena.

In the following figure we can see that both the variables that imply the transfer of the coordinate axes appear, as well as the variables related to the vision of the event from a mobile observation point. That is, the variables corresponding to the right triangle.

Figure 4

If we consider that there is no movement and that the observer is fixed at the point (O), this observer WOULD SEE the Extension of the event located on the axis (K) and with a dimension equal to (E – F). But, if we now consider that the observer is moving and his reference coordinates are (K'), the VISION of the aforementioned event on these coordinates will have a dimension: (e – f). So we can say that the VISION of the event has BEEN TRANSFORMED. And this dimension of Extension is what the observer must operate with.

18.- IS THE RELATIONSHIP td/(tp) MAINTAINED WHEN THE MOBILE REFERENCE SYSTEM MOVES?

The doubt might arise if with this displacement of coordinates.

The relationship remains constant: td/tp, which allows us to measure the value of the Extension of the event. Using Geometry we can say yes, applying Thales' Theorem.

(NOTE: See the geometric explanation of Thales' Theorem in the second part of this study)

SECOND PART

This second part serves to expose the mathematical approaches and ideas that support the criteria that have been used in the first part, for the construction of the aforementioned formulas.

1.- CONDITIONS OF VALIDITY FOR THE VIEW OF THE EXTENSION OF AN EVENT FROM A MOBILE OBSERVATION POINT. SYNCHRONIZATION CONDITIONS.

Let's look at Figure 2. At a given instant it happens that: at point (E) in space an event appears and at this same instant the possible observer of this event is at point (F) in space.

From this initial instant begins the path of the light ray that carries the image of the event and the path of the observer who has to detect said event. Calling (tr) the time spent in the ray path and (td) the observer's path time, as the two paths must coincide at the observation point (O), we will impose as a synchronization condition:

(tr) = (td)

This is the condition that we will impose in the calculations that we will carry out below.

2.- MATHEMATICAL DEDUCTION OF THE RELATIONSHIP BETWEEN THE
OWN TIME OF THE EXTENSION OF THE EVENT AND THE TRAVEL TIME TO THE PLACE OF OBSERVATION

To relate the Proper Time (tp) of the Extension of the event, with the Displacement Time (td) we will apply the Pythagorean Theorem to the right triangle that we gave as a reference.

Requiring compliance with the Synchronization Condition:

(tr) = (td)

It allows us to replace (tr) with (td) with what we obtain:

Grouping terms we have:

We can transform the denominator in the following way:

Eliminating (c), gives as result

3.- DEMONSTRATION THAT BY MOVING THE VISION OF THE EXTENSION ON THE MOBILE REFERENCE SYSTEM, THE RELATIONSHIP BETWEEN THE (td) AND THE (tp) IS MAINTAINED.

To demonstrate this fulfillment we must remember Thales' Theorem. We can say that in a right triangle the proportionality relationship between the path of the horizontal leg and the vertical leg is fulfilled.

Let us remember that in the vertical leg we will represent the Extension (tp) of the Event and in the horizontal leg the travel time of the observer.

The following figure aims to demonstrate the validity of this theorem, by observing that the aforementioned proportions are maintained

Figure 5

4.- DEMONSTRATION THAT THE SECOND FACTOR OF THE NUMERATOR OF THE TIME FORMULA CAN BE TRANSLATED AS A TIME

When exposing the formula for the transformation of time we said that the expression: (v×X)/c² is nothing more than the expression of a “time”. 

Let's prove this statement.

In the VISION of an event, which we use a mobile Reference System (SRM) with respect to a Fixed Reference System (SRF), it must be taken into account that we use two types of speeds of a completely different nature. Let us remember that it is about: (v) and (c). 

We must homologate these two concepts if we want to incorporate them in the execution of the same physical phenomenon. We use the speed of light (c) as measurement pattern. That is, the 300,000 km/sec. as a unit of speed.

To make the aforementioned conversions we must take into account the following criteria to follow:

All lengths will be quantified using: “light speed units” (uvl).

This means that: the (uvl) are those that would be consumed to move between two certain reference points. For example, we can write: x = k (uvl) meaning that a certain length (x) is found, or would require k (uvl) to reach it.

A relationship such as: (v/c) assigns a fraction of (uvl) to a given velocity (v), since (c) is a fixed quantity taken as a unit, while (v) is the relative velocity between Inertial Reference Systems, different value in each specific case.

To quantify a length (l) we will apply the expression: l = x.( v /c)

This expression answers the question: A length (x) that has been traveled at speed (v) is equivalent to what length (l) if the speed were that of light (c)?

To obtain the travel time (td) of a Mobile Reference System (MRS) on the axis (X), operating with (uvl), we must divide the space (l) by the speed of light (c).
I mean:

(td) = (l) / (c) 

and since 

l = x.( v /c)

we obtain: 

(td) = (l) / (c) = ( x).(v / c) / (c) = ((x).(v))/c²

THEORY OF SPECIAL RELATIVITY - A MISINTERPRETATION THAT LEADS TO NONSENSE

PRESENTATION

Although in previous studies published in our Blog, we have used the ideas that we will now comment on, we believe that it will be interesting to combine these concepts and highlight the mistaken idea that has led to accepting the Theory of Special Relativity as valid.

We remember that one of the texts that we have taken as a basis for our criticism is A. Einstein's book entitled: “On the theory of special and general relativity.

AN ERROR THAT CAUSES A SHOOTING

We will first expose an error of interpretation in the mental experiments proposed by A. Einstein to demonstrate his theory, whose interpretation leads to the absurdity of having to accept a transmutation of matter.

 

1.- THE ERROR OF IDENTIFYING THE VISION OF A PHYSICAL PHENOMENON WITH THE CHANGE IN NATURE OF THE SAME

In one of our previous essays we said the following:

“In the mental experiments taken from the aforementioned book by

Einstein, we will accept his conclusion as valid using the verb SEE instead of using the verb BE that the author uses in his approach and conclusion.

By this we mean that we agree that the physical phenomena that occur within a Mobile Reference System (MRS) when OBSERVED from another Fixed Reference System (RFS) can BE modified. This modification will affect the VISION dimension of its duration, or the dimension of its mass. But what we do not accept is the use of the verb SER. We should not interpret that the phenomenon that occurs within the Mobile Reference System (SRM) when observed from the Fixed Reference System (SRF) has been transformed”

We can say the same if the physical phenomenon occurs within a Fixed Reference System (SRF) and is SEEN or observed from a Mobile Reference System (SRM).

The following figure is the typical drawing in which a train car appears moving at a constant speed. There is a mirror on the ceiling. A person inside the car shoots a beam of light at the mirror. This ray is reflected in the mirror and returns to its place of origin.

This phenomenon of reflection of the light ray serves to confuse analysts of the subject of relativity of movements, to say that the duration of the path of the rebound of the light ray, for the person who is outside the car (SRF), is has lengthened with respect to the peron that is inside (SRM) and that has fired the beam.

The person outside the car (SRF) SEES the lengthening of the beam path. His SUBJECTIVE opinion is that he believes that the duration of the ray's path has lengthened. But this would be confusing the verb SEE with the verb BE.

The physical phenomenon of this reflection of the light ray has a single Proper Time (tp). For the ground-fixed observer (SRF) its

Rating will depend on the speed of the wagon. But, we repeat: We should not interpret that the phenomenon that occurs within the Mobile Recency System (SRM) when observed from the Fixed Reference System (SRF) has been transformed.

"THE METAPHOR OF THE THEORY OF SPECIAL RELATIVITY"

We now include a drawing that we devised and published in one of our studios to make a simile with the erroneous acceptance of the Theory of Relativity.

The drawing wants to materialize and represent the vision in a deformed mirror of the image that I intend to SEE. It is intended to be a comparison with the acceptance of the fallacies preached by the Theory of Special Relativity.

Following this theory makes us look in a convex mirror that distorts our ideas just as it would our image. We must look at ourselves in a flat mirror to really see our image and not believe in the “miracle” of transmutations. It is about SEEING correctly and not attributing to BEING what you SEE.

(In the previously mentioned case of the train car, it is its movement and its displacement that are equivalent to the concave mirror)

 

2.- THE ERROR OF TRYING TO FIND A DIFFERENCE BETWEEN TWO IDENTICAL AND SIMULTANEOUS EVENTS

In the aforementioned book by A. Einstein, in one of his epigraphs he exposes the topic of: The relativity of simultaneity. To which we criticize and say: “the error of the relativity of simultaneity.”

In the present study we criticize the conclusion drawn from the mental experiment presented by A. Einstein, in which he associates relative movements with events that are SIMULTANEOUS.

The WRONG conclusion that A. Einstein draws from this experiment, we will see, is the basis of the fallacy that we will discuss in the next issue.

We comment below on the mental experiment with which he intends to justify that two events that occur simultaneously ARE different depending on whether they are observed from the (SRF) or from the (SRM). We insist on stating that they WILL look different, but this does not mean that they change the quality of SIMULTANEOUSNESS that they have at the beginning of their production.

He asks in his book:

“Two events, for example, two lightning bolts (A) and (B), which are simultaneous with respect to the embankment, are

also simultaneous with respect to the train?”

(Refers to the embankment located on the tracks where the train car circulates)

And he goes on to say:

“…When we say that rays (A) and (B) are simultaneous with respect to the paths, we mean that the rays of light that leave places (A) and (B) meet at the midpoint (M) of the section of road (A)-(B). Now, do events (A) and (B) also correspond in places (A) and (B) on the train?

In order to better understand this question that A. Einstein asks, we have designed a drawing that represents a diagram of the mental experiment and its result.

The following drawing presents three phases of the wagon's progress. In it we make appear the two LIGHTNING FLASHES (A) and (B) and the RAYS OF LIGHT (A') and (B') that emerge from it

                

In this drawing we have made the rays reach the ground and we have drawn a person at the midpoint (M') of the distance between the rays.

As it appears in the drawing, and based on Einstein's conclusion, the person who is on the ground perceives the arrival of the light from the two simultaneous rays at the same moment, while the person who is riding the train perceives it sooner. the ray (B) than the ray (A). With this argument he affirms that the phenomenon of SIMULTANEOUSNESS IS different contemplated from the (SRF) than contemplated from the (SRM)

Here he makes the mistake that we have already mentioned and that the phenomenon is not deformed. In this case the SIMULTANEOUSNESS of the two events.

We can add that the relative movement to which the physical phenomenon is subjected deforms the VISION of the quality of the event. But the reality is that a SIMULTANEOUS circumstance (or let's call it phenomenon) has occurred. And this is what the person fixed on the ground (SRF) will judge.

Let us note that we are now presenting an inverse case to the one we had presented in the previous issue. There the phenomenon had occurred inside the car and it was the person who was on the outside of it (SRF) who SAW the phenomenon deformed, while the person who was inside (SRM) was the one who could really appreciate the phenomenon.

In the case that we are now discussing, the event occurs outside the carriage and it is the person inside it who WOULD see the SIMULTANEOUSNESS of the event distorted. It is the person who is outside (SRF) who can appreciate the circumstance of simultaneity as it IS.

Taking into account that the relative movement considered in the aforementioned mental experiments is nothing more than a disturbing effect of the VISION of the phenomenon, as we have seen we can consider examples where the quality of SIMULTANEOUSNESS of two events can occur both outside (SRF) as within the (SRM).

We give another example of a SIMULTANEOUSNESS phenomenon in which this circumstance occurs within the (SRM). We have devised a thought experiment, with relative movements between the train car and a fixed observer outside the car, and where the event of SIMULTANEOUSNESS occurs inside the car.

The drawing represents three phases of advance of a wagon that goes at a straight and constant speed.

In the center of the car there is a person holding a dough in each of his hands. The masses have equal weight. Outside the car there is a fixed observer on the ground (SRF).

Due to the movement of the wagon, at the moment that the person inside passes in front of the observer who is on the ground, that person releases the two masses at the same time. We consider this as a SIMULTANEOUS event.

We observe that in the intermediate step of the drawing it is seen that the masses have not yet touched the floor of the car. In the last stage represented by the drawing, the masses have already arrived on the ground. This is what the observer WOULD SEE (SRF)

The observer who is fixed on the ground (SRF) WILL SEE the different phases in which the masses fall, in the different phases of the wagon's advance.

The (SRF) WILL SEE the fall in each of the stages, while the (SRM) will consider a free fall.

It is evident that the SIMULTANEOUS fall of the two masses has not been transformed for the (SRF). YOU WILL SEE it deformed. It is the same thing that we had commented on the phenomenon of reflection in the mirror of the ray of light.

 

3.- THE PARADOX OF TRANSMUTATION

To help interpret and understand the metaphorical meaning given to the title of this issue, we transcribe the following definition and explanation: “PARADOX: Fact or saying contrary to logic.” “TRANSMUTATION: It involves the change of atomic nuclei. “It changes one element into another.”

The physicist A. Einstein, in his confusion of SEEING with BEING when dealing with the Relativity of Simultaneity, believes that an event produced in a (SRM) should not be IDENTIFY from an (SRF). And, in his aforementioned book, he mentions the following statement:

“The time needed for a process with respect to the wagon cannot be equated to the duration of the same process judged from the reference body of the embankment”

And, here the nonsense or the Paradox of Transmutation is born.

This is where we say that his statement is equivalent to the “miracle of transmutation. It does not admit that it LOOKS different but that it IS different.

Now he seems to forget the First Principle of relativity. He now speaks of “a” process “and not of the laws that govern natural phenomena. The confusion that he makes on the issue of the “relativity of simultaneity” makes him interpret the vision from the (SRF) of the events that occurred in the (SRM) differently.

To finish, we only need to remember the well-known “twin brother paradox”, in which the twin brother who stays on Earth spends more time than the astronaut brother.

Physics books call it a “paradox” when they want to justify the theory of special relativity and not find any logic to support it. We have read in one of these books that he proposes as a hypothesis that the interstellar rocket makes several revolutions before returning to Earth. What a joke! Let's keep in mind that the Theory of Special Relativity considers only rectilinear movements. Here, to resolve this paradox and using mental experiments, we can say that: the twin brother who is on Earth, with an astronomical telescope, SEES the course of the space rocket on which his astronaut brother is mounted. But this SEE does not imply a modification of the time or life cycle of each of the brothers.

In a future study we will give another grouping of essays.

 

 

THE MENTAL EXPERIMENT OF THE DEFLECTION OF LIGHT - A CONTRADICTION OF A. EINSTEIN

INTRODUCTION

In our previous essay we saw that, in the deflection of starlight, A. Einstein attributed it to the “deformation of space.” A nonsense. With this assumption it seemed that he found no other justification for committing such an aberration.

However, in the book by the authors: Albert Einstein and Leopold Infeld, entitled: “The Evolution of Physics”, we find that they give another justification for the aforementioned deflection of light. With this justification we ask ourselves: did A. Einstein change his mind about the cause of the deflection of starlight and abandon the fallacy of the “deformation of space”?... a scientific historian would have to inform us of the coincidence chronology of both opinions to clarify such contradiction.

The transcriptions that we make from the aforementioned book, or from other sources, will be written between quotation marks and in italics.

 

1.- A REMINDER OF OUR PREVIOUS ESSAY

In our previous essay titled: “The deformation of space – An error by A. Einstein”, we exposed the error made by this Physicist when considering that: “the Gravity caused by the sun curves space and this curvature causes the path to be deformed. of the light of the stars.” We call the phenomenon of curvature of the light path: deflection.

We present the fallacy of this approach in the aforementioned essay with the following comment and drawing taken from Google:

“Researchers thought that the Sun, due to its Gravity, would curve space, in such a way that this phenomenon would become noticeable in the perception of the position of starlight”

Faced with this thesis, which we demonstrate in the aforementioned essay to be a fallacy, A. Einstein seems to try to rectify his error by exposing that the deflection of starlight is caused directly by Gravity. Without involving “space” as a mediator.

This is what we will present, transcribing the mental experiment proposed in the book by the aforementioned authors: Albert Einstein and Leopold Infeld, entitled: “The evolution of physics”, on pages 177 and 178,

The conclusion of this thought experiment flies in the face of the claim that attributes the deflection of starlight to the warping of space.

 

2.- TRANSCRIPT OF THE TEXT OF THE MENTAL EXPERIMENT OF THE DEFLECTION OF LIGHT

Next, we will transcribe the text of the thought experiment that the aforementioned authors present in their book. In this transcription the reader will be able to see that his text is a bit tangled. We would say that it is rather “twisted”.

To help interpret the aforementioned thought experiment, in the following paragraph we will tell our own story. Now we will only dedicate ourselves to transcribing your text.

The text of the thought experiment described in the reference book talks about an elevator that “floats” in outer space. The elevator is pulled by a rope attached to its ceiling, which accelerates it. It says that there are two observers. One inside the elevator and one outside of it.

Its text is the following:

“Let's imagine that a horizontal ray of light enters the elevator through a side window, reaching the opposite wall after a very short time. Let's see how the path of light would be predicted by our observers."

The outside observer, who believes in the accelerated movement of the elevator, will argue: the light beam penetrates through the window, moving horizontally and in a straight line towards the opposite wall. But the elevator moves upward, changing position during the time the light lasts as it passes from one wall to the other. The ray will not illuminate, therefore, the point exactly opposite to that of its entrance, but rather a little lower. The difference, although very small, is real and consequently it turns out that the light moves with respect to the elevator on a curved line, like the figure we have drawn and not on the dotted line of the same figure.

The inner observer, who believes in the presence of a gravitational field acting on all the objects in his elevator, would say: the elevator has no such accelerated motion; A gravitational field simply acts inside it. A light beam that is imponderable will not be affected by gravity. If it propagates in a horizontal direction it will reach a point exactly opposite to that of its entrance.

It seems to emerge from this discussion that there is a possibility of deciding between both points of view, since the result would be different depending on whether one statement or the other was true. If there is nothing illogical in any of the reasoning that we have just presented, then all our previous argument falls to the ground, making it impossible, therefore, to consistently describe all the phenomena in question in two different ways: with or without a gravitational field.

But there is, fortunately, a serious error in the reasoning of the inner observer, which saves our conclusion. This said: “a light beam that is imponderable will not be affected by gravity. That's not true! A beam of light has energy and energy has mass. But all inert mass is attracted by a gravitational field since inert mass and gravitational mass are equivalent. A light beam will bend in a gravitational field exactly as would the trajectory of a body launched horizontally with a speed equal to that of light. Thus we see that, if the interior observer had reasoned correctly, taking into account the curvature of a light beam in a gravitational field, he would have arrived at the same result as the exterior observer.

 

3.- OUR ACCOUNT OF THE MENTAL EXPERIMENT THAT APPEARS IN THE MENTIONED BOOK.

To try to facilitate the understanding of the approach of the aforementioned mental experiment and at the same time declare an error that is committed in it, we have chosen to develop its content as if it were a story, giving it an argument.

We begin our story:

The thought experiment presents an elevator that ascends into outer space pulled by a rope. Ascends with accelerated speed:

Inside the elevator there is a person who we will identify as: PERSON INSIDE (PI).

Outside the elevator there is an observer who we will identify as: PERSON OUTSIDE (PE)

In our comments and opinions we will identify ourselves as: WE

We will identify the piece that belongs to the text of the experiment as NARRATOR.

A ray of light penetrates through the left wall of the elevator and ends its journey on the right wall.

The PE

He believes that the ascension of the elevator is what makes the curvature of light perceived.

US

We say that the (PE) is right in accepting the curvature of the ray of light.

But we contradict him, and say that he is NOT right in the cause he alleges. Later we will justify our opinion.

The (PI)

You don't realize that:

The rope is what moves the elevator. He attributes the fall of the masses (m) that are inside the elevator to the existence of a Gravitational field.

But he denies that the ray of light is curved due to Gravity and attributes it to a straight path.

STORYTELLER

The Narrator of the experiment says the following:

According to the above, there is a conflict between what they think (PE) and (PI).

The (PE) thinks that the ray of light bends.

The (PI) thinks that gravity cannot bend the path of a ray of light, although gravity acts on the masses (m) of the elevator.

US

In the end, the authors of the thought experiment to justify the validity of gravity exerting deflection on a ray of light, in their story, make the (PI) rectify their opinion. In their text they say the following:

“…But there is, fortunately, a serious error in the reasoning of the inner observer, which saves our conclusion. This said: “a light beam that is imponderable will not be affected by gravity.”

And now, putting an end to this “novel” they say the following:

“A beam of light has energy and energy has mass. But all inert mass is attracted by a gravitational field since inert mass and gravitational mass are equivalent. A light beam will bend in a gravitational field exactly as would the trajectory of a body launched horizontally with a speed equal to that of light. Thus we see that, if the interior observer had reasoned correctly, taking into account the curvature of a light beam in a gravitational field, he would have arrived at the same result as the exterior observer.

So “everyone is happy” and thus the deflection of a ray of light due to Gravity is justified. And nothing has been said about the “deformation of space”…

 

4.- AN ERROR IN APPROACH IN THE EXHIBITION OF THE MENTAL EXPERIMENT OF THE ELEVATOR

We have said that the (PE) affirms that the ray of light bends, but that it is not right with the reason it affirms for why it occurs. In the text of the book it is said that the (PE) believes that the ascension of the elevator is what makes it accepted that the curvature of light exists. This cause is NOT correct. It is a false opinion. All that was left was to mask this thought experiment with incorrect reasoning!…

We justify this error as follows:

If we consider a real case, in which we are the observer outside the elevator (PE) and as such the judges of the result of the observation, an error in approach is to consider that it is the ray of light that moves downwards. , when, on the contrary, it is the elevator that goes up. This seems to us to be a hoax by the authors of the aforementioned book to try to make their twisted arguments square, which later contradict each other by making Gravity intervene.

To graphically express our opinion, we have broken down the figure that we gave previously into three visions of the elevator's ascension.

The ray of light that enters from the left side of the elevator has been drawn. In the first view of the drawing, we place the entrance height of the beam at a higher level of the elevator. In the second vision the beam is approaching the middle part of the elevator, and in the third vision the beam is touching the floor.

Thus we visualize that it is not the ray that curves towards the floor of the elevator, but rather the elevator that goes up. Another issue is that the ray is curved by the action of Gravity.